Link de la siguiente applet: https://www.geogebra.org/m/cbmj4vns
Medidas de tendencia central
Nivel educativo al que va dirigida: Decimo y undecimo
Objetivos de aprendizaje
- Identificar la relación de las propiedades conceptuales
- Resolver problemas relacionados con los aspectos estadístico y abstracto.
- Comprender las propiedades relacionadas con los conceptos de la media aritmética
- Adquirir destreza con herramientas TIC
de tendencia central; en donde, se evidenciara el uso de fórmulas requeridas para resolver
una actividad que se encuentra en este medio o herramienta tecnológica; la cual, empodera
el aprendizaje significativo de las matemáticas con el uso de las TIC.
Entonces el alumno utilizando estos recursos responderá a la actividad.
Medidas de tendencia central
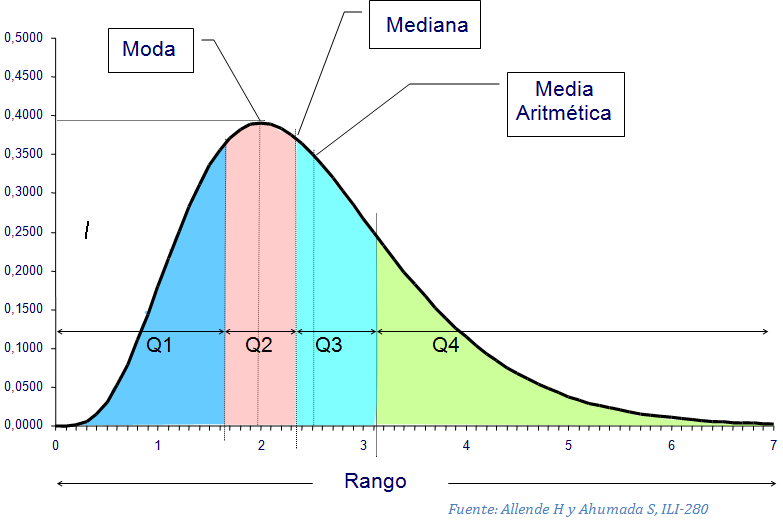
La media aritmética
Es el promedio o medición de tendencia central de uso más común. Se calcula sumando
todas las observaciones de una serie de datos y luego dividiendo el total entre el número
de elementos involucrados.
La expresión algebraica puede describirse como:
Donde N es el número de datos
Donde N es el número de datos
Un ejemplo:
Calcular la media de 2, 4, 6, 7, 9
N= 5 (el número de datos)
Aplicó la fórmula y queda la sumatoria de 2, 4, 6, 7 y 9, siendo igual a 28, dividido
por la cantidad de datos, es decir, dividido por 5. La media, entonces, es igual a 5,6.
La mediana
Es el valor medio de una secuencia ordenada de datos. Si no hay empates, la mitad
de las observaciones serán menores y la otra mitad serán mayores. La mediana no se
ve afectada por ninguna observación extrema de una serie de datos. Por tanto, siempre
que esté presente una observación extrema es apropiado usar la mediana en vez de la
media para describir una serie de datos.
Para calcular la mediana de una serie de datos recolectados en su forma sin procesar,
Para calcular la mediana de una serie de datos recolectados en su forma sin procesar, primero debemos poner los datos en una clasificación ordenada. Después usamos la
fórmula de punto de posicionamiento:
Para encontrar el lugar de la clasificación ordenada que corresponde al valor de la mediana,
Para encontrar el lugar de la clasificación ordenada que corresponde al valor de la mediana, se sigue una de las dos reglas:
Si el tamaño de la muestra es un número impar, la mediana se representa mediante
el valor numérico correspondiente al punto de posicionamiento, la observación
ordenada es (n+1)/2.
el valor numérico correspondiente al punto de posicionamiento, la observación
ordenada es (n+1)/2.
Si el tamaño de la muestra es un número par entonces el punto de posicionamiento
cae entre las dos observaciones medias de la clasificación ordenada. La mediana es
el promedio de los valores numéricos correspondientes a estas dos observaciones medias.
cae entre las dos observaciones medias de la clasificación ordenada. La mediana es
el promedio de los valores numéricos correspondientes a estas dos observaciones medias.
La moda
Es el valor de una serie de datos que aparece con más frecuencia. Se obtiene fácilmente
Es el valor de una serie de datos que aparece con más frecuencia. Se obtiene fácilmente de una clasificación ordenada. A diferencia de la media aritmética, la moda no se ve afectada
por la ocurrencia de los valores extremos.
Ejemplo:
Los valores siguientes son las calificaciones de un alumno durante todo el año
7; 8; 9; 7; 9; 8; 8; 8; 7; 8
Podemos afirmar entonces que el modo es igual a 8, dado que es el valor que
aparece con más frecuencia.
El rango medio
Es el promedio de las observaciones menores y mayores de una serie de datos.
El rango medio a menudo es usado como una medición de resumen tanto por analistas
financieros como por reporteros meteorológicos, puesto que puede proporcionar una
medición adecuada, rápida y simple para caracterizar toda una serie de datos, como por
ejemplo todo una serie de lecturas registradas de temperatura por horas durante todo un día.
El eje medio
Es el promedio del primer y tercer cuartil de una serie de datos. Es decir:
Eje medio: (Q1 + Q2) / 2
Siendo Q1 y Q2, el primer y segundo cuartil. En conclusión podemos decir que es una
medición de resumen usada para zanjar problemas potenciales introducidos por los
valores extremos de los datos.
Link de la siguiente applet: https://www.geogebra.org/m/cbmj4vns
Actividad encontrar media, mediana y moda con cada uno de los datos suministrados a continuación
Ficha para el alumno al que va dirigida
| ACTIVIDAD EDUCATIVA | |||||||||||||||||||||||||||||||
| Nombre: | |||||||||||||||||||||||||||||||
| Área: | Matemáticas | Grado: | Décimo y undécimo | ||||||||||||||||||||||||||||
| Fecha | Calificación: | ||||||||||||||||||||||||||||||
| APLIQUEMOS LO APRENDIDO | |||||||||||||||||||||||||||||||
| Tema: | Medidas de tendencia central | ||||||||||||||||||||||||||||||
| Subtema: | Resolución los problemas apoyados de la herramienta tecnológica | ||||||||||||||||||||||||||||||
| Actividad | Individual | ||||||||||||||||||||||||||||||
| Observaciones |
| ||||||||||||||||||||||||||||||
| Ejercicios | Ingresa a la aplicación geogebra y desarrolla los siguientes ejercicios:
Con cada uno de los siguientes datos y utilizando los recursos de geobra encuentre la media, mediana y moda.
|
Anexo video guia de como resolver los ejercicios de la actividad
Referencias bibliográficas: geogebra; recuperado de: https://www.geogebra.org/classic?lang=es Calculo der media, mediana y moda; recuperado de: https://youtu.be/ps3LAofi9x8
No hay comentarios:
Publicar un comentario